Differential Privacy
Randomized Response Surveys
Before the age of big data and data science, traditional data collection faced the challenge called the evasive answer bias. That is to say, people not answering survey questions honestly in fear that their answers may be used against them. Randomized responses emerged in the mid-twentieth century to address this.
Randomized response is a technique to protect the privacy of individuals in surveys. It involves adding local noise, such as flipping a coin multiple times and assigning the responses of the individual based on the coin-flip sequence. In doing so, the responses can be true in expectation but any given response is uncertain. This uncertainty over the response of an individual is one of the first applications of differential privacy, although it was not called as such at the time and the quantification of privacy was simply the weighting of probabilities determined by the mechanism.
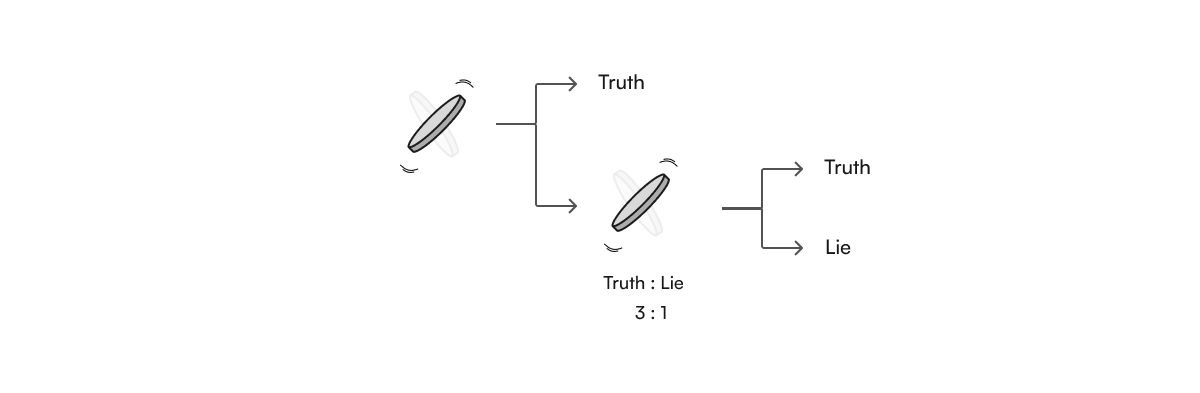
This approach of randomizing the output of the answer to a question by a mechanism, a stochastic intervention such as coin flipping, is still the very backbone of differential privacy today.
(The original approach by S.L. Warner actually involved spinning a “spinner” and as such he could easily change the weighting of the outcome based on the proportion of the circle assigned to each outcome. Whether you prefer a mental model of a roulette wheel, a spinner, coins flipping or dice rolling, as long as we can portray a well calibrated stochastic mechanism which is biased towards the truth, then the approach will work.)
ϵ-Differential Privacy
Pure epsilon-differential privacy ϵ-DP is a mathematical guarantee that enables the sharing of aggregated statistics about a dataset while protecting individual privacy by adding random noise. Simply put, it ensures that the outcome of any analysis is nearly the same, regardless of whether any individual’s data is either included or removed from the dataset.
Formally, the privacy guarantee is quantified using the privacy parameter ϵ (epsilon). A randomized algorithm \(A\) is ϵ-differentially private if for all neighboring datasets \(D_1\) and \(D_2\) (differing in at most one element), and for all subsets of outputs \(S \subseteq \text{Range}(M)\)
\[\Pr[M(D_1) \in S] \leq e^{\epsilon} \cdot \Pr[M(D_2) \in S]\]This \(M\) algorithm will provide a set amount of noise, quantified by ϵ, which would generate outputs with certain error from the real value, which can be quantified by the following interactive widget.
Randomized Response was ε-Differential Privacy
Although randomized response surveys predate the formal definition of differential privacy by over 40 years, the technique directly maps to the binary mechanism used in modern differential privacy.
Assume you wish to set up the spinner originally proposed by Warner to achieve ε-differential privacy. This can be done by asking participants to tell the truth with probability \(\frac{e^{\frac{\epsilon}{2}}}{1 + e^{\frac{\epsilon}{2}}}\). This is known in the literature as the binary mechanism.
This mechanism is incredibly useful for building intuition among a non-technical audience. One of the simplest questions we can ask is: “Is Alice in this dataset?” Depending on the level of privacy, the probability of answering truthfully will vary. We illustrate this relationship below.
| ε | Probability of Truth | Odds of Truth |
|---|
While the above odds are merely illustrative, they help convey the practical meaning of epsilon in relation to the more intuitive randomized response mechanism. As a point of reference, theorists often advocate for \(\epsilon \approx 1\) for differential privacy guarantees to have a meaningful privacy assurance.
Intuition of the Laplace Mechanism
One of the most widely used mechanisms in ε-differential privacy is the Laplace mechanism. It is used when we are adding bounded values together such as counts or summations of private values, provided the extreme values (usually referenced as bounds) of the private values are known and hence the maximum contribution of any data subject is bounded.
In practice, the true sum is first computed, then noise is sampled from the Laplace distribution, and finally this noise is added to the result. For example, if you’re counting and all the values lie within range in (0, 1), the widget below shows how the distribution of noise and expected error change as ε varies.
Note that the error is additive and so we can make claims about the absolute error, but not the relative error of the final stochastic result.
(ε, δ)-Differential Privacy
(ε, δ)-differential privacy is a mathematical guarantee that extends the concept of pure epsilon-differential privacy by allowing for a small probability of failure, with a second privacy parameter \(\delta\). Just as we described pure DP in our previous section, it also ensures that the outcome of any analysis is nearly the same, regardless of whether any individual’s data is present, but further includes a small allowance for a cryptographically small chance of error.
Formally, the privacy guarantee is now quantified using both \(\epsilon\) (epsilon) and also \(\delta\) (delta). A randomized algorithm \(M\) is \((\epsilon, \delta)\)-differentially private if for all neighboring datasets \(D_1\) and \(D_2\) (differing in at most one element), and for all subsets of outputs \(S \subseteq \text{Range}(M)\)
\[\Pr[M(D_1) \in S] \leq e^{\epsilon} \cdot \Pr[M(D_2) \in S] + \delta\]The following widget describes the expected error for noise added under (ε, δ)-DP.
Zero-Concentrated Differential Privacy
Zero-Concentrated Differential Privacy (zCDP) introduces a parameter \(\rho\) (rho) to measure the concentration of privacy loss around its expected value, enabling tighter control over cumulative privacy loss in repeated or iterative analyses. This makes zCDP particularly useful in applications that require multiple queries or iterative data use.
Formally, a randomized algorithm \(M\) satisfies \(\rho\)-zCDP such that for neighboring datasets \(D_1\) and \(D_2\) (differing in at most one element), and for all \(\alpha\) in (1, ∞), the following holds:
\[D_{\alpha}(M(D_1) \parallel M(D_2)) \leq \rho \alpha\]